통계적 가설 검정을 통한 두 집단의 변화 비교

통계적 가설 검정이란 ?

통계적 가설 검정(statistical hypothesis test)은 통계적 추측의 하나로서, 모집단 실제의 값이 얼마가 된다는 주장과 관련해, 표본의 정보를 사용해서 가설의 합당성 여부를 판정하는 과정을 의미한다.

통계적 가설 검정 절차

  1. 귀무가설과 대립가설 설정
    • 귀무가설 : 두 집단의 변화가 없다는 가설 (ex. A 집단과 B 집단의 평균키가 같다)
    • 대립가설 : 귀무가설이 기각되면 채택되는 가설로 두 집단의 변화가 있다는 가설 (ex. A 집단과 B 집단의 평균키가 다르다)
  2. 유의수준의 결정
    • p-value : 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률
    • 유의수준을 5% 로 설정하면 p-value 는 0.05
  3. 검정통계량 산출
    • 표본의 특성에 맞는 통계 분석법을 통해 검정통계량 산출 (ex. t-value, u-value, p-value)
  4. 통계적인 의사결정
    • 산출한 검정통계량 값을 통해 귀무가설을 채택할지 기각할지 결정
    • p-value 가 유의수준보다 같거나 높으면 귀무가설 채택 (대립가설 기각)
    • p-value 가 유의수준보다 낮으면 귀무가설 기각 (대립가설 채택) - 결국 표본을 통한 추정이기 때문에 채택/기각 판단이 100% 맞다고 보장할 수 없음

독립 표본 T 검정(Students`s T Test)

독립 표본 T 검정이란 ?

두 집단 간의 평균을 비교하는 모수적 통계방법으로 표본이 정규성, 등분산성, 독립성 등을 만족할 경우 적용 가능한 통계 분석법이다.

T 분포란 ?

  • 정규 분포의 평균을 측정할 때 사용하는 분포
  • 모집단이 정규분포라는 정도만 알고, 모분산을 모를 때 표본분산으로 대체하여 모 평균을 구할 때 사용
  • 적은 표본으로도 모집단 평균을 추정하려고 정규분포 대신 사용
  • 표준정규분포에 비해 꼬리가 두꺼움
  • 자유도가 증가할수록 표준정규분포에 가까워짐(중심극한정리)

t-value 산출

아래 공식을 통해 t-value 산출

p-value 산출

t 분포표를 통해 p-value 산출, 자유도와 t-value 에 해당하는 확률 값을 찾음

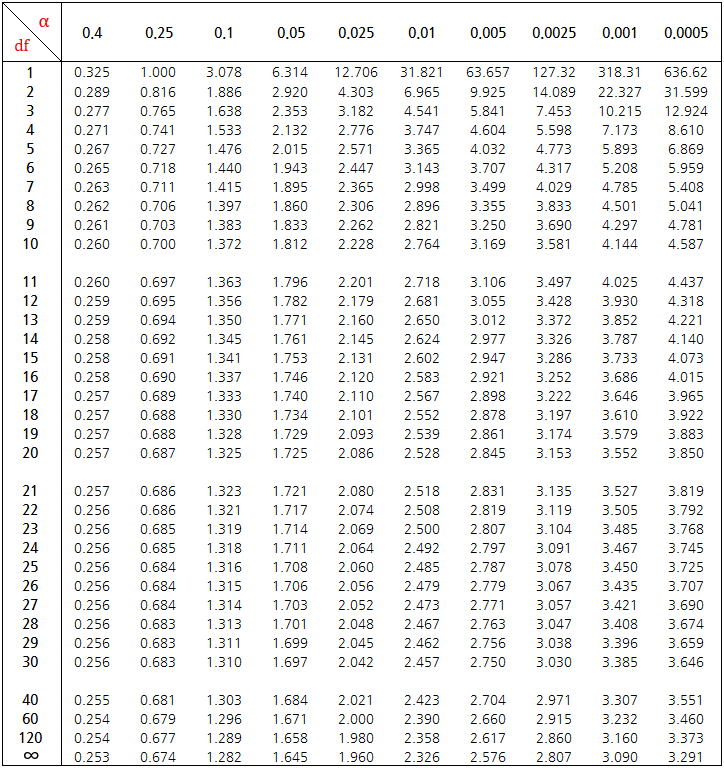
df = 자유도, a = 확률, cell 값 = t-value

python 을 통한 독립 표본 T 검정

from scipy import stats
import pandas as pd

data_a = pd.read_csv(a_path).iloc[0]
data_b = pd.read_csv(b_path).iloc[0]

t_result = stats.ttest_ind_from_stats(data_b['mean'], data_b['std'], data_b['size'], data_a['mean'], data_a['std'], data_a['size'], equal_var=False)

print(t_result)

t_result 를 출력하면 t-value 와 p-value 를 확인할 수 있다.
p-value 와 초기 설정한 유의수준의 비교를 통해 귀무가설의 채택/기각 여부를 결정할 수 있다.
또한 대립가설이 채택되었을 때 t-value 부호값을 통해 두개 그룹의 평균이 다른 경우 어떤 그룹의 값이 더 큰지 확인할 수 있다.